Segmentación utilizando K-means en Python

La segmentación con técnicas estadísticas es muy usada en diversos problemas. En marketing son útiles los modelos estadísticos para segmentar o dividir poblaciones en grupos distintos. Esto permite realizar campañas diferentes a cada uno de los grupos. Los modelos estadísticos de segmentación también son empleados en procesamiento de imágenes así como en algoritmos de compresión de imágenes. En general, los algoritmos de segmentación agrupan datos similares usando una serie de variables.

En este artículo voy a hablar de uno de los métodos estadísticos más empleados para segmentar, el algoritmo k-means o k-medias.

El algoritmo k-means es un método de agrupamiento que divide un conjunto de n observaciones en k grupos distintos gracias a valores medios. Pertenece al ámbito de los algoritmos no supervisados, ya que las n observaciones no cuentan con una etiqueta que nos diga de qué grupo es cada dato, siendo los datos agrupados según sus propiedades o características.

El agrupamiento de las n observaciones en los k grupos distintos se realiza minimizando la suma de distancias entre cada observación y el centroide de su grupo o clúster. La distancia más común es la distancia euclídea.

¿Cómo funciona k-means?:

---

El algoritmo cuenta con tres pasos:

1. Inicialización: una vez escogido k (número de grupos), se establecen los centroides en el espacio de los datos, por ejemplo asignando los k puntos aleatoriamente.
2. Asignación de las observaciones a los centroides: cada observación es asignada al centroide más cercano a ella usando la medida de distancia que se determine.
3. Actualización de los centroides: se actualiza la posición de los centroides de cada grupo tomando como posición la media de la localización de las observaciones de dicho grupo.

Se repiten los pasos 2 y 3 hasta que los centroides se quedan fijos, o se mueven por debajo de una distancia umbral fijada.

El algoritmo k-means es un algoritmo de optimización cuyo objetivo es minimizar la suma de distancias cuadráticas de cada observación al centroide de su clúster.

Las n observaciones se pueden representar como un vector real de d dimensiones, tantas como variables o características que representan cada observación. El algoritmo k-means utiliza las n observaciones \((x_1,x_2,…,x_n)\) para construir k grupos donde minimiza la suma de distancias de las observaciones dentro de cada grupo \(S=\{S_1,S_2,…,S_k\}\) a su centroide.

$$
\underset{\mathbf{S}}{\mathrm{min}}\; E\left(\boldsymbol{\mu_{i}}\right)=\underset{\mathbf{S}}{\mathrm{min}}\sum_{i=1}^{k}\sum_{\mathbf{x}_{j}\in S_i}\left\Vert \mathbf{x}_{j}-\boldsymbol{\mu}_{i}\right\Vert ^{2}
\quad$$

siendo S el conjunto de datos cuyos elementos son las observaciones \(x_j\) representados por vectores, donde cada uno de sus elementos representa una característica o atributo. Tendremos k grupos o clústers con su correspondiente centroide \(\boldsymbol{\mu_{i}}\).

En cada actualización de los centroides se impone la condición necesaria de extremo a la función \(E\left(\boldsymbol{\mu_{i}}\right)\) que para la función cuadrática es:

$$
\frac{\partial E}{\partial\boldsymbol{\mu}_{i}}=0\;\Longrightarrow\;\boldsymbol{\mu}_{i}^{(t+1)}=\frac{1}{\left|S_{i}^{(t)}\right|}\sum_{\mathbf{x}_{j}\in S_{i}^{(t)}}\mathbf{x}_{j}
$$

y se calcula cada nuevo centroide como el promedio de los elemento de cada grupo.

Para utilizar el algoritmo k-means es necesario definir el número de grupos k, la medida de distancia utilizada y la inicialización de los centroides. En general no converge a un mínimo global, sino a un mínimo local.

Casos de uso del algoritmo k-means:

---

Los algoritmos no supervisados de clustering como k-means pueden ser usados para encontrar grupos ocultos en los datos, o intuidos pero no etiquetados. Pueden servir para confirmar o desterrar alguna asunción sobre los datos. También son usados para descubrir relaciones entre los datos, que de manera manual no podríamos haber obtenido.

Una vez se ejecuta el algoritmo y obtenidos sus grupos o etiquetas, se puede pasar a un problema de aprendizaje supervisado. Es decir, asignando a cada grupo una clase distinta.

Entre los casos de uso se encuentran:

• Segmentación de usuarios/clientes basado en el comportamiento: utilizando datos como el comportamiento web, el patrón de consumo… se pueden agrupar clientes o usuarios en distintos grupos.
• Categorización de inventario: agrupando productos por su patrón de venta.
• Detección de anomalías: según el comportamiento web es posible diferenciar distintos grupos. Por ejemplo, usuarios humanos, bots, arañas web o trolls.

¿Cómo elegir el valor de k (número de grupos)?:

---

Aunque el algoritmo k-means pertenece a los algoritmos denominados como no supervisados, es necesario seleccionar un valor k del número de grupos en los que se agrupan los datos. En general, no hay una forma exacta de determinar el número de grupos, pero se pueden usar ciertas reglas o estadísticos que nos ayudan a estimar el número de grupos:

1- El método del codo:

La idea básica de los algoritmos de clustering es la minimización de la varianza intra-cluster y la maximización de la varianza inter-cluster. Es decir, queremos que cada observación se encuentre muy cerca a las de su mismo grupo y los grupos lo más lejos posible entre ellos.

El método del codo utiliza la distancia media de las observaciones a su centroide. Es decir, se fija en las distancias intra-cluster. Cuanto más grande es el número de clusters k, la varianza intra-cluster tiende a disminuir. Cuanto menor es la distancia intra-cluster mejor, ya que significa que los clústers son más compactos. El método del codo busca el valor k que satisfaga que un incremento de k, no mejore sustancialmente la distancia media intra-cluster.

El método del codo es a veces ambiguo, una alternativa es el análisis de la silueta, que es más objetivo que el método del codo.

2- Análisis de la silueta:

El análisis de la silueta mide la calidad del agrupamiento o clustering. Mide la distancia de separación entre los clústers. Nos indica como de cerca está cada punto de un clúster a puntos de los clústers vecinos. Esta medida de distancia se encuentra en el rango [-1, 1]. Un valor alto indica un buen clustering.

Los coeficientes de silueta cercanos a +1 indican que la observación se encuentra lejos de los clústers vecinos. Un valor del coeficiente de 0 indica que la observación está muy cerca o en la frontera de decisión entre dos clústers. Valores negativos indican que esas muestras quizás estén asignadas al clúster erróneo.

El método de la silueta calcula la media de los coeficientes de silueta de todas las observaciones para diferentes valores de k. El número óptimo de clústers k es aquel que maximiza la media de los coeficientes de silueta para un rango de valores de k.

El coeficiente de la silueta es calculado como:

$$S = \frac{b-a}{max(a,b)}$$

siendo a la distancia media intra-clúster y b la distancia media a las observaciones del clúster más cercano.

Elección de la distancia usando k-means:

---

La elección de la distancia para los problemas de clustering es de gran importancia ya que cambiar la medida de similaridad entre elementos impacta en el cálculo de los clústers.

Las distancias más clásicas usadas en algoritmos de clusters son:

1. Distancia euclídea
   $$d_{euc}(x,y) = \sqrt{\sum_{i=1}^n(x_i – y_i)^2}$$
2. Distancia Manhattan
   $$d_{man}(x,y) = \sum_{i=1}^n |{(x_i – y_i)|}$$
3. Distancia de correlación de Pearson
   $$d_{cor}(x, y) = 1 – \frac{\sum\limits_{i=1}^n (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum\limits_{i=1}^n(x_i – \bar{x})^2 \sum\limits_{i=1}^n(y_i -\bar{y})^2}}$$
4. Distancia de correlación de coseno
   $$d_{eisen}(x, y) = 1 – \frac{\left|\sum\limits_{i=1}^n x_iy_i\right|}{\sqrt{\sum\limits_{i=1}^n x^2_i \sum\limits_{i=1}^n y^2_i}}$$
   siendo x e y dos vector de longitud n.

La distancia usada por defecto es la distancia euclídea. Dependiendo del tipo de datos y de las preguntas que se quieren responder, se pueden preferir otras medidas de distancia. Por ejemplo, la distancia de correlación es muy usada en análisis de expresión de genes.

La correlación de Pearson es muy sensible a outliers o valores atípicos. Esto puede ser mitigado usando en su lugar la correlación de Spearman, en lugar de la de Pearson.

Si escogemos la distancia euclídea, las observaciones con valores altos de variables serán agrupadas juntas. Igualmente con valores bajos de variables.

Preprocesamiento de datos para utilizar k-means:

---

Las variables o características que de los datos deben ser valores numéricos, continuos en la medida de lo posible. En caso de ser categóricos, se pueden intentar pasarlos a valores numéricos aunque no es recomendable ya que no existe una distancia «real».

Del mismo modo es recomendable escalar los valores y no introducir variables muy correlacionadas o que sean combinaciones lineares de otras variables. Es decir, hay que evitar la multicolinearidad.

El objetivo de escalar las variables es el de hacer que sean comparables. Generalmente las variables se escalan para tener:

1. Media igual a cero
2. Desviación típica igual a uno

Este método de escalado se denomina «estandarización» y se consigue usando la siguiente fórmula:

$$Z(x) = \frac{x_i – centro(x)}{desviacion(x)}$$

centro (x) es una medida de centralidad como la media o mediana y desviación (x) es una medida de dispersión como la desviación típica o el rango intercuartílico.

La estandarización de los datos es importante ya que hace que cuatro métodos de distancias – euclídea, Manhattan, correlación y eisen – sean más similares que sin escalar.

Ejemplo de uso de k-means usando Python:

---

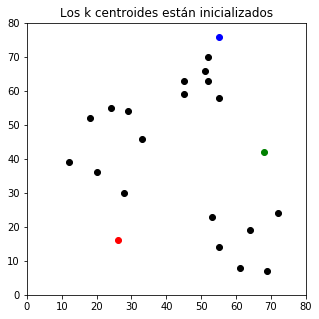
Primeramente asignamos un valor k al número de grupos que queremos tener e inicializamos los centroides en valores aleatorios:

---

## Inicialización

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

df = pd.DataFrame({
    'x1': [12, 20, 28, 18, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 64, 69, 72],
    'x2': [39, 36, 30, 52, 54, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 19, 7, 24]
})

np.random.seed(200)
# Número de centroides k = 3
k = 3 
# Inicializamos los centroides a valores aleatorios en el espacio de datos
centroids = {
    i+1: [np.random.randint(0, 80), np.random.randint(0, 80)]
    for i in range(k)
}
    
fig = plt.figure(figsize=(5, 5))
plt.scatter(df['x1'], df['x2'], color='k')
colmap = {1: 'r', 2: 'g', 3: 'b'}
for i in centroids.keys():
    plt.scatter(*centroids[i], color=colmap[i])
plt.title(u'Los k centroides están inicializados')
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()

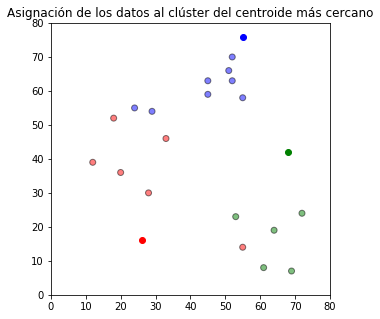
Posteriormente, cada observación se asigna al grupo del centroide más cercano.

---

## Asignación de las observaciones a los centroides

def asignacion(df, centroids):
    for i in centroids.keys():
        # sqrt((x1 - c1)^2 - (x2 - c2)^2)
        df['distance_from_{}'.format(i)] = (
            np.sqrt(
                (df['x1'] - centroids[i][0]) ** 2
                + (df['x2'] - centroids[i][1]) ** 2
            )
        )
    centroid_distance_cols = ['distance_from_{}'.format(i) for i in centroids.keys()]
    df['closest'] = df.loc[:, centroid_distance_cols].idxmin(axis=1)
    df['closest'] = df['closest'].map(lambda x: int(x.lstrip('distance_from_')))
    df['color'] = df['closest'].map(lambda x: colmap[x])
    return df

df = asignacion(df, centroids)

fig = plt.figure(figsize=(5, 5))
plt.scatter(df['x1'], df['x2'], color=df['color'], alpha=0.5, edgecolor='k')
for i in centroids.keys():
    plt.scatter(*centroids[i], color=colmap[i])
plt.title(u'Asignación de los datos al clúster del centroide más cercano')
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()

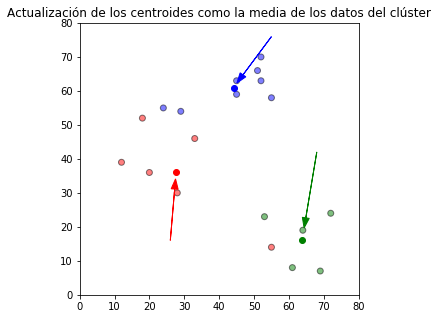
Con los valores de las observaciones de los grupos se calculan y actualizan los nuevos centroides de cada grupo.

---

## Actualización de los centroides

import copy

old_centroids = copy.deepcopy(centroids)

def update(k):
    for i in centroids.keys():
        centroids[i][0] = np.mean(df[df['closest'] == i]['x1'])
        centroids[i][1] = np.mean(df[df['closest'] == i]['x2'])
    return k

centroids = update(centroids)
    
fig = plt.figure(figsize=(5, 5))
ax = plt.axes()
plt.scatter(df['x1'], df['x2'], color=df['color'], alpha=0.5, edgecolor='k')
for i in centroids.keys():
    plt.scatter(*centroids[i], color=colmap[i])
plt.title(u'Actualización de los centroides como la media de los datos del clúster')
plt.xlim(0, 80)
plt.ylim(0, 80)
for i in old_centroids.keys():
    old_x = old_centroids[i][0]
    old_y = old_centroids[i][1]
    dx = (centroids[i][0] - old_centroids[i][0]) * 0.75
    dy = (centroids[i][1] - old_centroids[i][1]) * 0.75
    ax.arrow(old_x, old_y, dx, dy, head_width=2, head_length=3, fc=colmap[i], ec=colmap[i])
plt.show()

Y se asignan nuevamente las observaciones al grupo del centroide más cercano a ellas.

---

## Repetición de la asignación de las observaciones al centroide más cercano

df = asignacion(df, centroids)

# Representación de resultados
fig = plt.figure(figsize=(5, 5))
plt.scatter(df['x1'], df['x2'], color=df['color'], alpha=0.5, edgecolor='k')
for i in centroids.keys():
    plt.scatter(*centroids[i], color=colmap[i])
plt.title(u'Repetición de la asignación de las observaciones al centroide más cercano')
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()

 

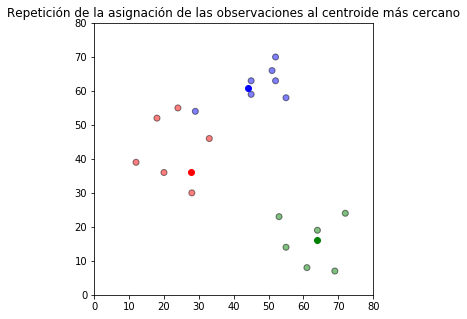
Estos dos últimos pasos se repiten iterativamente hasta un criterio de parada en el que se estabilizan los grupos.

 

Si te ha sido de utilidad este post, te agradecería que me apoyases en Patreon (donando una cantidad aunque sea poca ya sea una vez, o apoyándome mensualmente). Tener una web, dominio, hosting, no es gratis y me apoyas a seguir ayudando con la difusión de educación libre. Apóyame en Patreon! Mil gracias!!