¿Cómo saber si una variable sigue una distribución normal en Python?
16 octubre 2020Saber si una variable sigue una distribución normal o no es muy importante en ciertos problemas de ciencia de datos y aprendizaje automático. Existen ciertos tests que nos permiten comprobar si una distribución sigue una forma normal o Gaussiana.
Funciones de distribución
Primero de todo quiero definir lo que es una función de distribución, para partir de la misma base todos. La función de distribución de una variable aleatoria es una función que especifica la probabilidad de que los valores observados de la variable se encuentren en cualquier región dada de valores posibles.
Ejemplos de funciones de distribución que pueden seguir las variables
Distribución normal o Gaussiana
La distribución normal (también llamada Gaussiana) es la más utilizada en estadística. Es muy común encontrarse variables que siguen distribuciones normales en fenómenos de la naturaleza. Una variable que se distribuye de manera normal tiene un histograma (función de densidad) con forma de campana, con un pico y es simétrica alrededor de la media. Existen términos como la curtosis o la asimetría de la distribución que se utilizan a menudo para describir cómo se desvía una distribución de la normalidad.
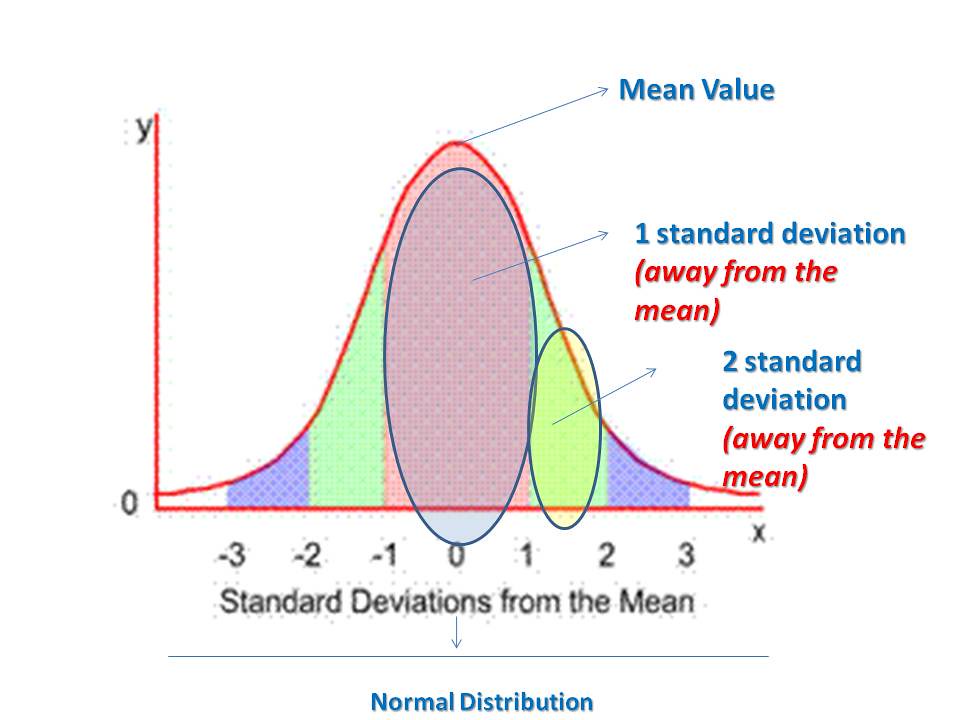
Representación de una función de distribución normal
Una característica de la función de distribución normal es que la media, moda y mediana son iguales.
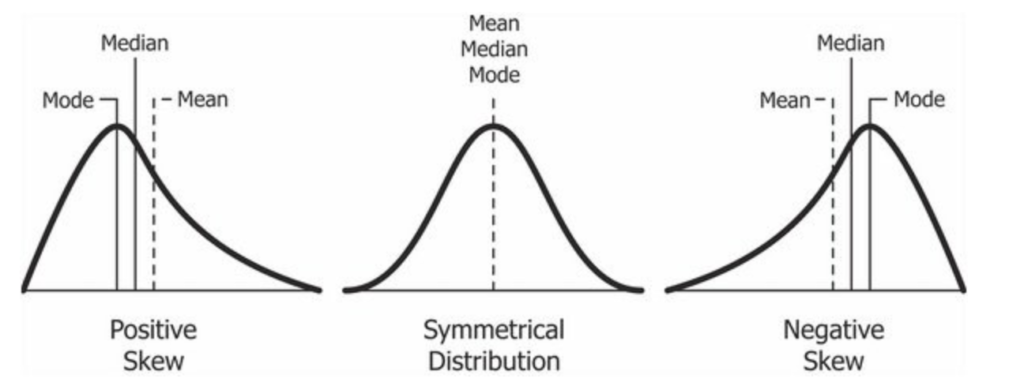
Medidas de asimetría de una variable (Skewness)
Vale Álvaro, ¿Por qué todo este rollo de las distribuciones normales y no normales? ¿Por qué es importante la distribución Normal o Gaussiana? La distribución Normal o Gaussiana es importante en ciencia de datos ya que existen algoritmos y procedimientos estadísticos paramétricos que suponen que las variables de entrada siguen una distribución normal. Por ello, es necesario comprobar si nuestras variables siguen una distribución normal. En caso de no seguirla, se hace necesario realizar alguna transformación de la variable como la transformación Box-Cox.
¿Cómo saber si mi variable sigue una distribución normal en Python?
Con histogramas:
Simplemente representando la distribución de la variable con un histograma podemos ver si la variable sigue una distribución normal. En el histograma, los datos se dividen en un número predeterminado de grupos llamados bins o cajas. Luego, los datos se clasifican en cada caja y se obtiene el recuento del número de observaciones en cada caja.
from numpy.random import seed, randn
import matplotlib.pyplot as plt
# Configuro la semilla aleatoria
seed(1993)
# Genero 100 muestras
distribucion_generada = randn(100)
# Represento el histograma
plt.hist(distribucion_generada )
plt.title('Histograma de una variable')
plt.xlabel('Valor de la variable')
plt.ylabel('Conteo')
plt.show()
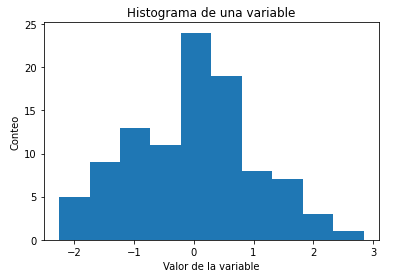
Histograma de una variable generada en Python
Con la representación de cuantíles teóricos (Q-Q plot):
El segundo método es unos de mis favoritos y se trata del gráfico Q-Q. Esta gráfica genera su propia muestra de la distribución con la que estamos comparando, en este caso la distribución normal o gausiana. Las muestras se dividen en grupos, llamados cuantiles. Cada punto de datos de la muestra se empareja con un miembro similar de la distribución con la que comparamos en la misma distribución de acumulación.
Los puntos resultantes se trazan como un diagrama de dispersión con el valor comparativo en el eje x y la muestra de datos en el eje y. Una línea de puntos en un ángulo de 45 grados desde la parte inferior izquierda del gráfico hasta la parte superior derecha mostrará una coincidencia perfecta con la distribución con la que comparamos. A menudo, se traza una línea para ver más clara esa diferencia. Las desviaciones de los puntos de la línea muestran una desviación de la distribución esperada.
from numpy.random import seed, randn import matplotlib.pyplot as plt from statsmodels.graphics.gofplots import qqplot # Configuro la semilla aleatoria seed(1993) # Genero 100 muestras distribucion_generada = randn(100) # Represento el Q-Q plot qqplot(distribucion_generada , line='s') plt.show()
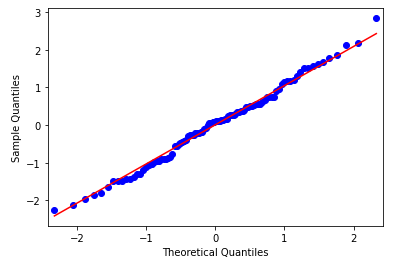
En el caso anterior, la distribución generada podemos decir que es normal ya que sigue casi a la perfección la línea roja.
La prueba de Shapiro-Wilk:
Este es es un ejemplo de test de hipótesis para saber si una distribución sigue la forma de otra distribución.
La prueba de Shapiro-Wilk es una prueba bastante buena para comprobar la normalidad de una variable. Se sugiere que la prueba se utilice para muestras de datos pequeñas, miles de observaciones o menos. En caso de tener más observaciones
from numpy.random import seed, randn
import matplotlib.pyplot as plt
from scipy.stats import shapiro
# Configuro la semilla aleatoria
seed(1993)
# Genero 100 muestras
data = randn(100)
# Prueba de Shapiro-Wilk
stat, p = shapiro(data)
print('Estadisticos=%.3f, p=%.3f' % (stat, p))
# Interpretación
alpha = 0.05
if p > alpha:
print('La muestra parece Gaussiana o Normal (no se rechaza la hipótesis nula H0)')
else:
print('La muestra no parece Gaussiana o Normal(se rechaza la hipótesis nula H0)')
Estadisticos=0.991, p=0.755
La muestra parece Gaussiana o Normal (no se rechaza la hipótesis nula H0)
Prueba K^2 de D’Agostino
La prueba K^2 de D’Agostino calcula curtosis y asimetría a partir de los datos, para determinar si la distribución de datos se aparta de la distribución normal.
from numpy.random import seed, randn
import matplotlib.pyplot as plt
from scipy.stats import normaltest
# Configuro la semilla aleatoria
seed(1993)
# Genero 100 muestras
data = randn(100)
# Test de DAgostino
stat, p = normaltest(data)
print('Estadisticos=%.3f, p=%.3f' % (stat, p))
# Interpretación
alpha = 0.05
if p > alpha:
print('La muestra parece Gaussiana o Normal (no se rechaza la hipótesis nula H0)')
else:
print('La muestra no parece Gaussiana o Normal(se rechaza la hipótesis nula H0)')
Estadisticos=0.326, p=0.850
La muestra parece Gaussiana o Normal (no se rechaza la hipótesis nula H0)
Espero que os haya sido útil este artículo. Si quieres compartir con nosotros cualquier método o sugerencia, déjanos un comentario. Nos vemos en siguientes posts! 🙂
Si te ha sido de utilidad este post, te agradecería que me apoyases en Patreon (donando una cantidad aunque sea poca ya sea una vez, o apoyándome mensualmente). Tener una web, dominio, hosting, no es gratis y me apoyas a seguir ayudando con la difusión de educación libre. Apóyame en Patreon! Mil gracias!!
¿Te ha parecido útil este artículo?


Buen artículo. Tengo una duda y quisiera saber si me puede ayudar.
En caso de trabajar con pequeñas cantidades de datos (menos de 1000) y usar técnicas de machine learning (por ejemplo MLP). Se puede usar la prueba de Shapiro Wilk para probar la normalidad de los residuos?
Muchas gracias.
Hola Marcelino. Se puede, aunque lo que más se suele usar es el QQplot
Buenas tardes Álvaro,
He leído un artículo suyo muy interesante hablando de los mejores másters de Big Data, Data Science y Machine Learning que hay en nuestro país y estoy bastante perdido sobre cual elegir en primer lugar, no se como contactar con usted por eso me he venido a este artículo para ver si me podría ayudar.
Le comento mi situación para ver si me puede ayudar, tengo 22 años y acabo este año la carrera de matemáticas y quería obtener un máster en dicho campo. Me gustaría realizar un máster más bien práctico pero no sé si especializado en big data o en data science, creo que está algo más demandado los especialistas en data scientist y igual me decantaría por ese lado un poco más.
He visto el máster que oferta ICAI, estuve viendo sus comentarios hacia otras personas y ponía que era bastante completo y abarcaba ambos temas. Después también me gusta el mundo de las finanzas pero tampoco sé si hacer un master tan específico como sería hacerlo en AFI o en CUNEF.
Vi otras posibilidades que eran ESIC y EAE por si sabría algo acerca de estas dos (aunque de EAE ya leí un poco de que no sabía totalmente como era el programa).
Por último, quería saber su opinión sobre si merece la pena realizar el máster en una universidad privada debido a los contactos y a la bolsa de empleo ( ya sea IE, ICADE, EAE…) respecto a universidades publicas.
Un saludo y perdón por las molestias ocasionadas,
Alejandro.
Hola Alejandro, disculpame pero todo lo que sea consejo y guía de carrera no lo contesto porque consume mucho tiempo y es algo que necesitaría saber muchos detalles, etc.
Genial artículo. Estadística explicada muy claramente.
Gracias
Muchas gracias por tu comentario Iñaki!
Gracias, excelente explicación, sintética y de aplicación práctica
Gracias a ti Freddy por seguirnos!