
Regresión lineal en Python
15 junio 2018En este artículo hablaré sobre la regresión lineal, seguramente el algoritmo más sencillo de aprendizaje supervisado dentro del paradigma del machine learning. Como ya comentamos en un post anterior, hay cuatro tipos de aprendizaje: supervisado, no supervisado, semi-supervisado y aprendizaje por refuerzo.
Dentro de los supervisados se encuentra la regresión lineal, que es una herramienta útil para predecir una respuesta cuantitativa.
Existen muchos algoritmos posteriores que pueden ser vistos como una generalización o una extensión de las regresiones lineales, por ello es importante tener un conocimiento real de este algoritmo, aunque pueda parecer simple.
En sentido amplio lo que hace una regresión lineal es obtener la relación entre unas variables independientes (\(X\)) y una variable dependiente (\(Y\)). Es decir, teniendo una serie de variables predictoras obtiene la relación con una variable cuantitativa a predecir. La regresión lineal explica la variable \(Y\) con las variables \(X\), y obtiene la función lineal que mejor se ajusta o explica esta relación.
Regresión lineal simple
Introducción al modelo
La regresión lineal simple parte de una sóla variable predictora, es decir \(X=x_1 \:donde \:X \in \mathbb{R} \) y supone que existe aproximadamente una relación lineal entre X e Y. Esta relación lineal puede ser escrita como:
$$Y=\underbrace{\beta_0+\beta_{1}X}_{modelo}+\underbrace{\epsilon}_{error}$$
Es decir, Y es igual a X multiplicado por un coeficiente más un coeficiente de offset y un término de error. La parte \(\beta_0+\beta_{1}X\) es el modelo de regresión lineal, siendo \(\beta_0\) y \(\beta_{1}\) los coeficientes de la regresión lineal y \(\epsilon\) el error cometido por el modelo.
Los términos \(\beta_0\) y \(\beta_1\) representan respectivamente el interceptor y la pendiente del modelo lineal. Son lo que se denomina coeficientes o parámetros del modelo de regresión lineal. Estos dos coeficientes son dos constantes que se obtienen por medio de lo que se denomina «entrenamiento» del modelo de regresión. Este entrenamiento se realiza con datos de los que sabemos valores reales de la tupla \((X,y)\). Una vez obtenida la estimación de estos dos coeficientes se puede predecir la variable Y usando X conocidos y a partir de la siguiente fórmula:
$$\hat{y}= \hat{\beta_0}+\hat{\beta_1}x$$
Siendo \(\hat{y}\) la predicción que obtenemos y \(\hat{\beta_0}\) y \(\hat{\beta_1}\) estimaciones obtenidas con el entrenamiento.
Si el término de error \(\epsilon\) es bajo para esta muestra, nuestra predicción será aproximadamente igual al valor real: $$\hat{y}\approx y$$
Por lo tanto, el entrenamiento y ajuste del modelo de regresión simple tratará de obtener los valores de \(\hat{\beta_0}\) y \(\hat{\beta_1}\) que mejor ajusten el modelo, es decir, mejor predigan el \(Y\) en función de \(X\).
Estimación de los coeficientes
Como hemos dicho antes, la estimación de los coeficientes se realiza con valores reales conocidos de la tupla \((X,y)\). Supongamos que tenemos \(n\) registros con variable independiente y dependiente conocidas:
$$(x_1,y_1),(x_2,y_2),…,(x_n,y_n)$$
Con estas n observaciones, el objetivo es obtener las estimaciones de los coeficientes \(\hat{\beta_0}\) y \(\hat{\beta_1}\) que hagan que el modelo lineal se ajuste lo mejor posible a los datos. Es decir, que \(y_i \approx \hat{\beta_0} + \hat{\beta_1} x_i \) para todos los \(x_i\), o lo que es lo mismo, encontrar la pendiente y la ordenada en el origen de la recta que pasa más cerca de los puntos \((x_i,y_i)\).
Esta medida de cercania entre la recta y los puntos se puede hacer de distintas formas, siendo la forma más común la de ajustar por mínimos cuadrados (less squares criterion).
Estimación por mínimos cuadrados
Siendo \(\hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_i \) las predicciones de \(y_i\), el residuo o diferencia entre la predicción y el valor real es:
$$r_i=y_i-\hat{y_i}$$
El método de mínimos cuadrados obtendrá los coeficientes que minimicen la suma de residuos al cuadrado, es decir, que minimicen:
$$RSS=\sum_{i=1}^{n}{r_i}^2$$
Usando derivadas parciales e igualando a 0 obtenemos que:
$$\left\{\begin{array}{1}\frac{\partial{RSS}}{\partial{\hat{\beta_1}}} = 0 \longrightarrow \hat{\beta_1} = \frac{\sum^{n}_{i=1}(x_i – \bar{x})(y_i – \bar{y})}{\sum^{n}_{i=1}(x_i – \bar{x})^2}\\\\
\frac{\partial{RSS}}{\partial{\hat{\beta_0}}} = 0 \longrightarrow \hat{\beta_0} = \bar{y} – \hat{\beta_1}\bar{x}\end{array}\right.$$
Siendo \(\bar{x}\) e \(\bar{y}\) las medias aritméticas de las muestras.
Ejemplo de regresión lineal simple usando Python
Primeramente creo un dataset de prueba, al que ajustaré un modelo de regresión lineal.
import numpy as np import random from sklearn import linear_model from sklearn.metrics import mean_squared_error, r2_score import matplotlib.pyplot as plt %matplotlib inline # Generador de distribución de datos para regresión lineal simple def generador_datos_simple(beta, muestras, desviacion): # Genero n (muestras) valores de x aleatorios entre 0 y 100 x = np.random.random(muestras) * 100 # Genero un error aleatorio gaussiano con desviación típica (desviacion) e = np.random.randn(muestras) * desviacion # Obtengo el y real como x*beta + error y = x * beta + e return x.reshape((muestras,1)), y.reshape((muestras,1)) # Parámetros de la distribución desviacion = 200 beta = 10 n = 50 x, y = generador_datos_simple(beta, n, desviacion) # Represento los datos generados plt.scatter(x, y) plt.show()
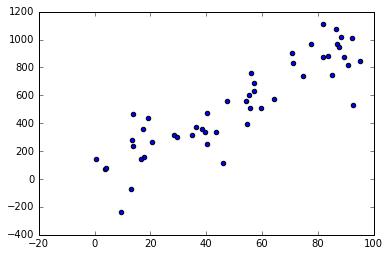
Generación de datos aleatorios
# Creo un modelo de regresión lineal modelo = linear_model.LinearRegression() # Entreno el modelo con los datos (X,Y) modelo.fit(x, y) # Ahora puedo obtener el coeficiente b_1 print u'Coeficiente beta1: ', modelo.coef_[0] # Podemos predecir usando el modelo y_pred = modelo.predict(x) # Por último, calculamos el error cuadrático medio y el estadístico R^2 print u'Error cuadrático medio: %.2f' % mean_squared_error(y, y_pred) print u'Estadístico R_2: %.2f' % r2_score(y, y_pred)
Coeficiente beta1: [ 9.89500401] Error cuadrático medio: 22140.95 Estadístico R_2: 0.79
# Representamos el ajuste (rojo) y la recta Y = beta*x (verde) plt.scatter(x, y) plt.plot(x, y_pred, color='red') x_real = np.array([0, 100]) y_real = x_real*beta plt.plot(x_real, y_real, color='green') plt.show()
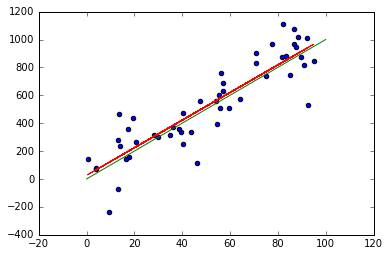
Ajustes de las rectas de regresión
Regresión lineal múltiple
Introducción al modelo
En la práctica solemos tener n variables predictoras, no sólo 1. Podríamos hacer n regresiones lineales simples, pero cada una de ellas ignoraría a las otras n-1 variables y no se sacaría ventaja de las relaciones entre variables.
La regresión lineal simple puede extenderse para el caso de n variables como:
$$Y=\underbrace{\beta_0+\beta_{1}X_1+\beta_{2}X_2+…+\beta_{n}X_n}_{modelo}+\underbrace{\epsilon}_{error}$$
En este caso a cada variable predictora le asignamos un coeficiente que marca la pendiente. Estos coeficientes \(\beta_i\) marcan la relación lineal entre \(Y\) y la variable \(X_i\). Se puede interpretar como el efecto medio en Y de un incremento de una unidad en \(X_i\), manteniendo el resto de variables predictoras fijas.
Estimación de los coeficientes
Análogamente a la regresión lineal simple, podemos obtener estimaciones \(\hat{\beta_i}\) de los coeficientes \(\beta_i\) mediante el entrenamiento y posteriormente hacer predicciones de Y usando la fórmula:
$$\hat{y}= \hat{\beta_0}+\hat{\beta_1}x_1+\hat{\beta_2}x_2+…+\hat{\beta_n}x_n$$
Estos parámetros son calculados usando una medida de cercanía como los cuadrados medios. Calculamos los \(\hat{\beta_i}\) que minimizan la suma de residuos al cuadrado:
$$RSS=\sum_{i=1}^{n}{r_i}^2 = \sum_{i=1}^{n}({y_i-\hat{y_i}})^2 = \sum_{i=1}^{n}({y_i-\hat{\beta_0}+\hat{\beta_1}x_{i1}+\hat{\beta_2}x_{i2}+…+\hat{\beta_n}x_{in}})^2$$
import numpy as np
import random
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
def generador_datos_multiple(coeficientes, muestras, std_dev):
# Calculamos el número de predictores y creamos una matriz
# con los coeficientes con p filas y 1 columna para
# multiplicación de matrices
n_coeficientes = len(coeficientes)
coef_matriz = np.array(coeficientes).reshape(n_coeficientes, 1)
# Igual que en el caso de regresión lineal simple
x = np.random.random_sample((muestras, n_coeficientes)) * 100
epsilon = np.random.randn(muestras) * std_dev
# Como x es una matriz muestras x n_coeficientes, y
# coef_matriz es n_coeficientes x 1
# Podemos hacer multiplicación de matrices para obtener y
# dados x1,x2,...,xn necesitamos hacer la transpuesta
# para obtener un array 1xmuestras en lugar de muestrasx1 para
# usar la regresión
y = np.matmul(x, coef_matriz).transpose() + epsilon
return x, y
# Genero los datos que ajustaré con la recta
coeficientes_reales =[10, 5]
muestras = 200
std_dev = 100
X, Y = generador_datos_multiple(coeficientes_reales, muestras, std_dev)
# Creo un modelo de regresión lineal
modelo = linear_model.LinearRegression()
# Entreno el modelo con los datos (X,Y)
modelo.fit(X, Y.transpose())
# Ahora puedo obtener el coeficiente b_1
print u'Coeficiente beta1: ', modelo.coef_[0]
# Podemos predecir usando el modelo
y_pred = modelo.predict(X)
# Por último, calculamos el error cuadrático medio y el estadístico R^2
print u'Error cuadrático medio: %.2f' \
% mean_squared_error(Y.transpose(), y_pred)
print u'Estadístico R_2: %.2f' % r2_score(Y.transpose(), y_pred)
Coeficiente beta1: [ 9.73631401 4.9061911 ] Error cuadrático medio: 8628.75 Estadístico R_2: 0.92
f, [p1, p2] = plt.subplots(1,2)
f.set_figwidth(15)
# Represento los puntos para la variable X1 y para Y
p1.scatter(X[:,0], Y)
p1.set_title(u'Representación de Y en función de X1')
p1.set_xlabel('X1')
p1.set_ylabel('Y')
p2.scatter(X[:,1], Y)
p2.set_title(u'Representación de Y en función de X2')
p2.set_xlabel('X2')
p2.set_ylabel('X')
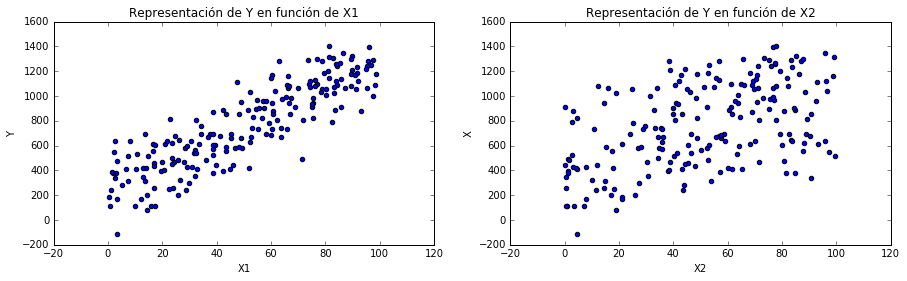
Generación de datos aleatorios de 2 variables independientes y 1 dependiente
# Represento la superficie que ajusta mejor a los datos
p3 = plt.figure(figsize=(15,10)).gca(projection='3d')
x1, x2 = np.meshgrid(range(100), range(100))
# Superficie que se obtiene con la regresión lineal múltiple
z_modelo = modelo.coef_[0][0]*x1 + modelo.coef_[0][1]*x2
# Superficie real de los datos
z_real = coeficientes_reales[0]*x1 + coeficientes_reales[1]*x2
# Represento ambas superficies
p3.plot_surface(x1, x2, z_modelo, alpha=0.3, color='green')
p3.plot_surface(x1, x2, z_real, alpha=0.3, color='yellow')
# Represento también los datos para ver el ajuste
p3.scatter(X[:,0], X[:,1], Y)
p3.set_title(u'Regresión lineal usando dos variables \
(X1,X2) para predecir Y')
p3.set_xlabel('Eje X1')
p3.set_ylabel('Eje X2')
p3.set_zlabel('Eje Y')
p3.view_init(10, )
plt.show()
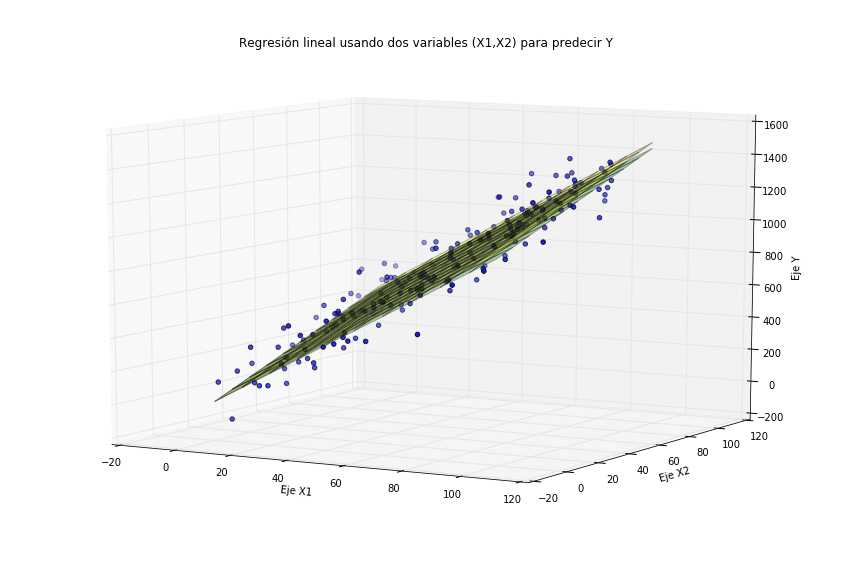
Ajuste de los dos hiperplanos a los datos
Evaluación de la precisión del modelo
La calidad del ajuste de la regresión lineal típicamente es evaluada usando dos medidas: el RSE (error estándar de los residuos o residual standard error) y el estadístico R cuadrado.
RSE
El RSE es una estimación de la desviación estándar del error \(\epsilon\). En otras palabras, es la cantidad media que la respuesta se desviará de la recta real de regresión. Se obtiene con la siguiente fórmula:
$$RSE = \sqrt{\frac{RSS}{(n – 2)}} = \sqrt{\frac{\sum_{i=1}^{n}{(y_i-\hat{y_i})}^2}{(n – 2)}}$$
Su valor puede ser bueno o malo dependiendo del contexto ya que no es adimensional. Si los valores son muy grandes, podremos obtener RSE enormes pero relativamente buenos ya que dependen de la dimensión de las Y. Independientemente, valores menores de RSE indican un mejor ajuste.
Coeficiente de determinación (R cuadrado)
El RSE, al ser una medida absoluta y medirse en unidades de Y, no es muy claro qué constituye un buen RSE. El \(R^2\) o coeficiente de determinación, sin embargo toma valores entre 0 y 1, representa la proporción de la varianza explicada y es independiente de la escala de Y.
Para calcular el \(R^2\) se usa la siguiente fórmula:
$$R^2 = \frac{TSS-RSS}{TSS} = 1 – \frac{RSS}{TSS}$$
siendo TSS (Total sum of squares) la suma total de errores cuadrados. Mide la varianza total de la respuesta Y. Su cálculo es:
$$TSS = \sum_{i=1}^{n}({y_{i} – \bar{y}})^2$$
RSS mide la variabilidad que queda sin explicar en el modelo. TSS mide la variabilidad inherente de Y antes de modelizar. Es decir, \(R^2\) mide la proporción de la variabilidad de Y que es explicada por el modelo. O dicho de otra forma, mide la proporción en términos de error cuadrático que nuestro modelo mejora a un modelo que simplemente diese como predicción para todas las y, la media \(\hat{y_i}=\bar{y}\).
Un valor de \(R^2\) cercano a 1 indica que una larga proporción de la variabilidad de Y está explicada o quitada gracias al modelo. Sin embargo, al igual que el RSE, depende de la aplicación lo que haga que un \(R^2\) sea bueno o no ya que hay problemas donde el error residual es pequeño y otros donde no lo es.
El estadístico \(R^2\) es una medida de la relación lineal entre X e Y. También lo es la correlación, cuya fórmula es:
$$r = Corr(X,Y) = \frac{\sum_{i=1}^{n}({x_{i} – \bar{x}})({y_{i} – \bar{y}})}{\sqrt{\sum_{i=1}^{n}({x_{i} – \bar{x}})^2}\sqrt{\sum_{i=1}^{n}({y_{i} – \bar{y}})^2}}$$
De hecho, en el caso de la regresión lineal simple se cumple que \(r^2=R^2\). Esto no ocurre en el caso de regresión lineal múltiple, ya que la correlación relaciona sólo un par de variables. Sin embargo el coeficiente \(R^2\) sigue siendo válido para casos multivariables.
Si te ha sido de utilidad este post, te agradecería que me apoyases en Patreon (donando una cantidad aunque sea poca ya sea una vez, o apoyándome mensualmente). Tener una web, dominio, hosting, no es gratis y me apoyas a seguir ayudando con la difusión de educación libre. Apóyame en Patreon! Mil gracias!!
¿Te ha parecido útil este artículo?


Alvaro felicitaciones, podrías ayudarme como graficar el b0,b1 en una regresión logistica.!
Buen contenido
Gracias Brenda!!
BUENAZO!
Bien resumido para aquellos con algo de conocimiento, como para aquellos que vienen de 0. Gracias.
Muchas gracias Luis! Me alegra que te haya gustado 🙂