
Problemas comunes en aprendizaje automático
10 mayo 2018Después de hablar de qué es el aprendizaje automático, es bueno hacerse una idea de los tipos de problemas más típicos que se presentan en el campo de la ciencia de datos. Saber identificar nuestro problema es ciertamente útil ya que de esa forma podremos saber cómo abordarlo y qué técnicas y algoritmos usar para ello.
Existen más tipos de problemas de los que trato en este post, pero estos unos de los más comunes:
Regresión
Los problemas de regresión se caracterizan en que la variable de respuesta \(Y\) es cuantitativa. Esto significa que la solución a nuestro problema es representada por una variable continua que puede ser flexiblemente determinada por las entradas \(X\) a nuestro modelo, en lugar de estar restringida a un grupo posible de valores. Ejemplos de variables cuantitativas pueden ser el salario y el peso de una persona.
Los problemas de regresión que tienen entradas con dependencia temporal son también llamados problemas de predicción de series temporales o forecasting. Un ejemplo de modelos que tratan estos problemas es el ARIMA, que permite a los científicos de datos explicar entre otras cosas la estacionalidad de las ventas, etc.
Los modelos de regresión predicen el valor de \(Y\) dados valores conocidos de variables \(X\). Las predicciones dentro de el rango de valores del dataset que se usa para ajustar el modelo reciben el nombre de interpolaciones. Por el contrario, aquella que están fuera del rango del dataset usado para ajustar o entrenar el modelo reciben el nombre de extrapolaciones.
La realización de extrapolaciones se basan fuertemente en supuestos. Cuanto más lejos esté la extrapolación de los datos, más espacio hay para fallos debido a las diferencias entre las suposiciones y la realidad.
Existen diferentes modelos que pueden ser usados para predecir una variable cuantitativa, siendo la regresión lineal de los más simples. En el caso de la regresión lineal, el algoritmo intenta ajustarse a los datos de la mejor forma obteniendo el hiperplano más optimo (por ejemplo, el que minimize la distancia cuadrática a los puntos). En el modelo más general de regresión lineal, llamado regresión lineal múltiple tenemos \(p\) variables independientes:
$$y_i=\beta_{1}x_{i1}+\beta_{2}x_{i2}+…+\beta_{p}x_{ip}+\epsilon_i$$
siendo \(y_i\) la respuesta \(i\), los términos \(\beta\) los coeficientes que se quieren calcular, \(x_i\) los valores de las variables independientes y \(\epsilon\) el término de error.
Ejemplo de un problema de regresión en Python
En este ejemplo genero una serie de datos \((x,y)\) y los modelizo con una regresión lineal simple:
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Generación de datos aleatorios
randGen = np.random.RandomState(1)
x = 10 * randGen.rand(50)
y = 2 * x - 5 + randGen.randn(50)
modelo = LinearRegression(fit_intercept=True)
modelo.fit(x[:, np.newaxis], y)
xAjuste = np.linspace(0, 10, 1000)
yAjuste = modelo.predict(xAjuste[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xAjuste, yAjuste)
plt.title(u'Regresión lineal')
plt.xlabel('x')
plt.ylabel('y');
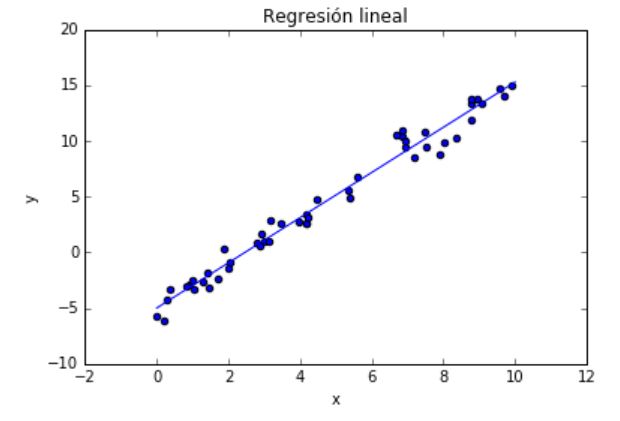
Ejemplo de problema de regresión
Clasificación
Los problemas de clasificación se caracterizan por tener una variable cualitativa \(Y\) como respuesta. Muchas veces las variables cualitativas también reciben el nombre de variables categóricas.
Al hecho de predecir una respuesta cualitativa de una observación se le llama clasificar dicha observación, es decir, predecir la categoría o clase de dicha observación.
Muchas veces los métodos encargados de clasificar lo que hacen es predecir la probabilidad de una observación de pertenecer a cada una de las categorías. En cierto modo se comportan también como algoritmos de regresión.
Entre los métodos de clasificación se encuentran:
- Regresión logística
- K-NN (K-nearest neighbors)
- SVMs
Aunque hay muchos más métodos para usar en clasificación.
Los problemas de clasificación quizás aparecen incluso más que los de regresión. Algunos podrían ser:
- Clasificar en clientes buenos y malos.
- Clasificar modelos de coches distintos
- Clasificación de muestras de ADN para determinar enfermedades.
En los problemas de clasificación tenemos un conjunto de tuplas \((X,Y)\), cuyas \(Y\) toman valores categóricos. Si suponemos que contamos con n observaciones tenemos:
$$(x_1,y_1),(x_2,y_2),…,(x_n,y_n)$$
tuplas con las que entrenar nuestro algoritmo de clasificación.
Generalmente estos problemas calculan la probabilidad de cada clase y luego esas probabilidades se mapean y se clasifican las observaciones. Para calcular las probabilidades, se debe obtener una función que transforme las entradas \(X\) en una salida que prediga la probabilidad de \(X\) para cierta clase. \(x \rightarrow f(x)= p(x)\)
Esta función debe hacer que las probabilidades de las clases estén lo más cerca posible al valor real de la clase. Es decir, supongamos que tenemos 2 clases posibles «clase A» y «clase B», si la muestra X tiene una Y=clase A, la función f debe ser tal que p(x) de la clase A sea cercana a 1 y p(x) de la clase B sea cercana a 0.
La función f tiene una serie de coeficientes \(\beta\) que se obtienen cumpliendo lo anterior. Uno de los métodos más generales es el de maximizar la función de verosimilitud utilizando los datos de entrenamiento (tuplas \((X,Y)\)). La función de verosimilitud es:
$$l(\beta)=\prod_{i:y_i=1}p(x_i)\prod_{i’:y_{i’}=0}(1-p(x_{i’}))$$
y los \(\beta\) serán los parámetros que maximicen \(l(\beta)\)
Ejemplo de un problema de clasificación en Python
En el siguiente ejemplo se muestra la línea de separación entre dos clases usando máquinas de soporte vectorial para clasificación (SVC) con un kernel lineal.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn import svm
X = np.array([[1,2],[5,8],[1.5,1.8],[8,8],[1,0.6],[9,11]])
y = [0,1,0,1,0,1]
clasificador = svm.SVC(kernel='linear', C = 1.0)
clasificador.fit(X,y)
w = clasificador.coef_[0]
print(w)
a = -w[0] / w[1]
xx = np.linspace(0,12)
yy = a * xx - clasificador.intercept_[0] / w[1]
h0 = plt.plot(xx, yy, 'k-', label=u'Linea de separación entre clases')
plt.scatter(X[:, 0], X[:, 1], c = y)
plt.scatter(10,4, color='green', marker='x')
plt.title(u'Linea de separación de las SVC con kernel lineal')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
print(u'La predicción de clase dada para el punto (10,4) es: %d' %clasificador.predict([[10,4]])[0])
[ 0.1380943 0.24462418]
La predicción de clase dada para el punto (10,4) es: 1
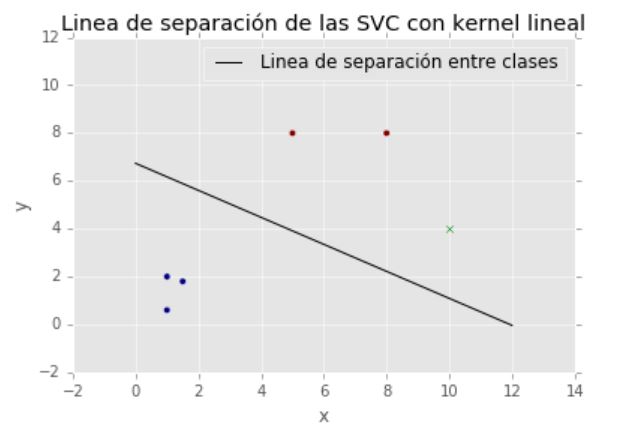
Separación con SVC de dos clases. El punto verde, que no pertenece al conjunto de entrenamiento, es asignado a la clase de los dos puntos rojos
Clustering
Los algoritmos de clustering o agrupamiento son un amplio conjunto de técnicas para encontrar subgrupos o clústers en los datos. Cuando agrupamos los datos queremos encontrar particiones que dividan los datos en grupos distintos pero homogéneos.
Es decir, queremos que los grupos sean lo más distintos posibles entre ellos pero que las muestras dentro de cada grupo sean similares.
Para alcanzar este objetivo hay que definir qué entendemos con que unas muestras sean similares o distintas. Esta definición de similaridad depende de conocimiento de los datos a estudiar.
Supongamos que tenemos \(p\) variables de \(n\) observaciones de enfermedades. Podríamos usar las técnicas de clustering para agrupar las \(n\) observaciones en grupos de enfermedades. Este es un problema no supervisado ya que intentamos obtener conocimiento de la estructura de los datos (en este caso grupos de datos).
Otra aplicación del clustering está en la segmentación de mercados usada en marketing, identificando grupos homogéneos de personas.
Ejemplo de un problema de clustering en Python
En este ejemplo se expone uno de los métodos más usados en la clusterización de datos, el método de K-Means o K-Medias. En este caso uso K=2, es decir, agrupo los datos en 2 grupos.
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from sklearn.cluster import KMeans
X = np.array([[5,3],
[10,15],
[15,12],
[24,10],
[30,45],
[85,70],
[71,80],
[60,78],
[55,52],
[80,91],])
plt.scatter(X[:,0],X[:,1], label='True Position')
plt.title(u'Puntos con los que hacer clustering')
plt.xlabel('x')
plt.ylabel('y');
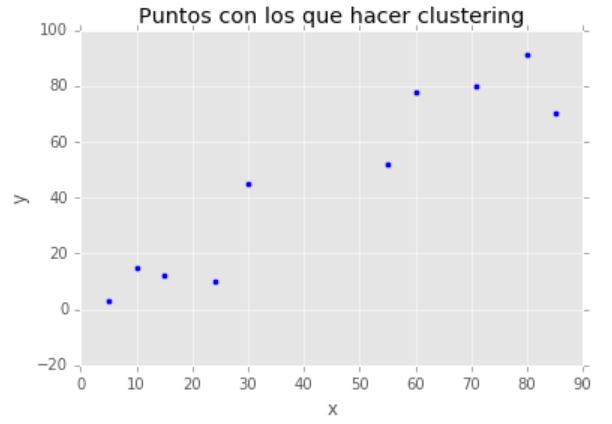
Puntos de partida a agrupar
kmeans = KMeans(n_clusters=2) kmeans.fit(X) print u'Coordenadas de los 2 centroides de los clústers: ', kmeans.cluster_centers_ print u'\nEtiquetas de clúster asignadas a los datos: ', kmeans.labels_
Coordenadas de los 2 centroides de los clústers: [[ 16.8 17. ][ 70.2 74.2]]
Etiquetas de clúster asignadas a los datos: [0 0 0 0 0 1 1 1 1 1]
plt.scatter(X[:,0],X[:,1], c=kmeans.labels_, cmap='rainbow')
plt.title(u'Puntos con la asignación de clúster')
plt.xlabel('x')
plt.ylabel('y');
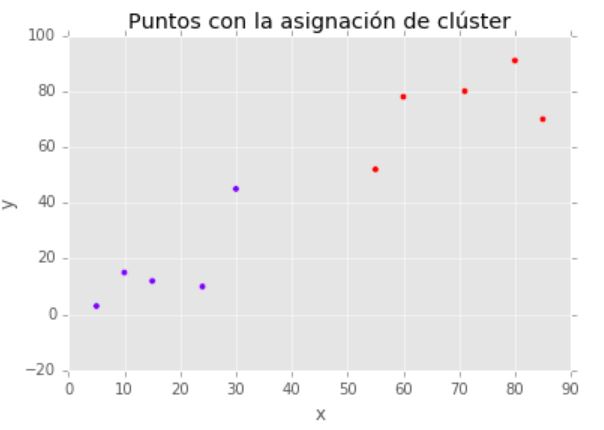
Clusterización en 2 grupos
Reducción de dimensionalidad
Los métodos de reducción de dimensionalidad son los procesos de reducir el número de variables obteniendo un subgrupo de variables principales. Puede ser dividido en selección de variables y en extracción de variables.
Estos métodos sirven para problemas donde se tienen una gran cantidad de variables y se pretende resumir o recopilarlas en otro grupo de variables más fácil de tratar.
Los métodos de reducción de dimensionalidad convierten la información de un dataset de gran dimensión en otro con menos dimensión asegurándose de que contiene información similar. Son usados típicamente en el proceso de resolución de problemas de Machine Learning.
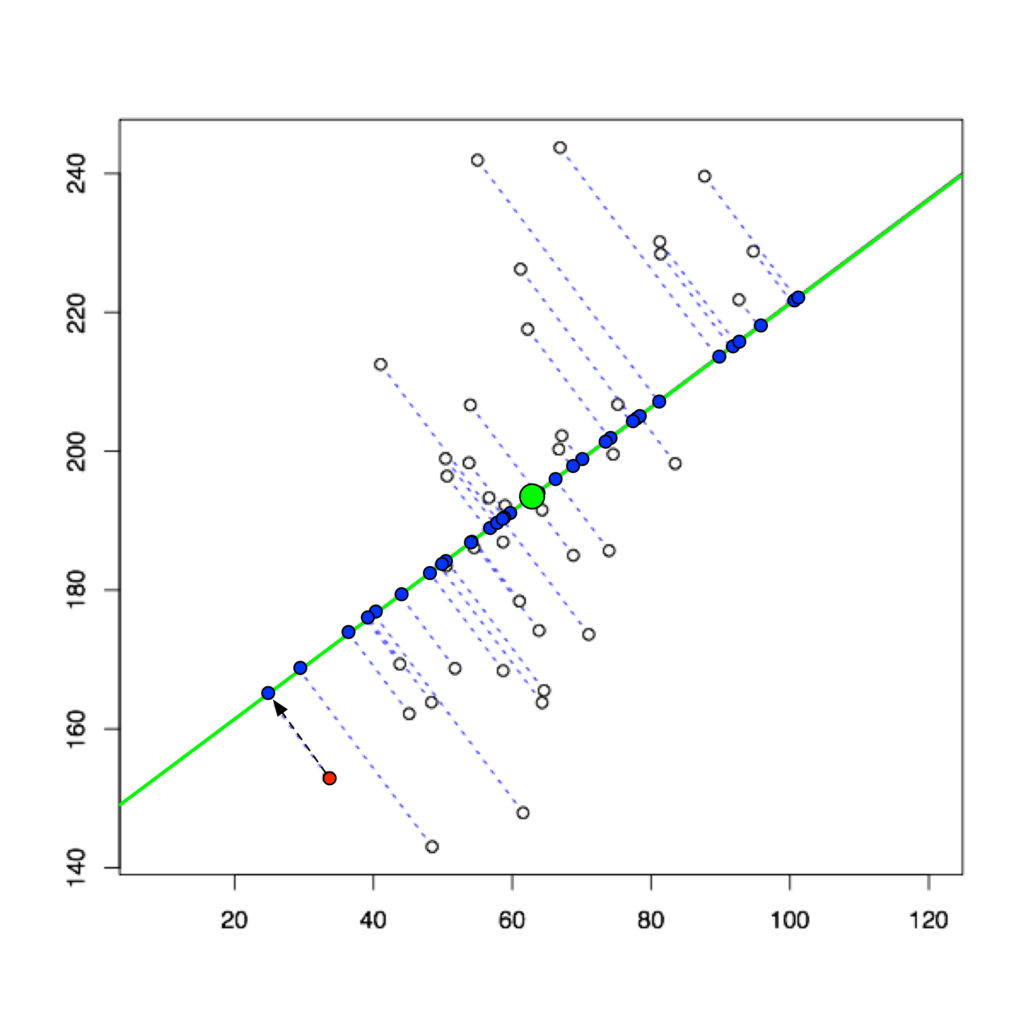
Ejemplo de PCA aplicado a 2 variables
Entre las ventajas de la reducción de dimensionalidad se encuentran:
- Comprime y reduce el espacio requerido para almacenar los datos.
- Mejora el tiempo de procesamiento para la realización de los mismos cálculos.
- Tiene en cuenta el efecto de multicolinearidad, borra o minimiza variables redundantes incrementando el rendimiento de los modelos.
- Puede reducir los datos a dimesiones representables como la 2D o 3D.
Estas ventajas son generales, siendo cada método de reducción de dimensionalidad distinto y siendo necesario de un estudio previo de cómo funcionan en particular.
Ejemplo de reducción de dimensionalidad en Python
En el siguiente ejemplo se muestra cómo se puede usar redimensión de dimensionalidad para explicar los datos de entrada con menos variables y sin perder apenas información. El algoritmo utilizado se denomina Análisis de Componentes Principales o PCA y es un ejemplo de métodos de extracción de variables.
import numpy as np from sklearn.decomposition import PCA X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) pca = PCA(n_components=2) pca.fit(X) print u'Relación de varianza explicada: ',pca.explained_variance_ratio_ print u'Componentes que representan el vector X: ',pca.components_
Relación de varianza explicada: [ 0.99244289 0.00755711]
Componentes que representan el vector X: [[-0.83849224 -0.54491354][ 0.54491354 -0.83849224]]
Enlaces de interés y bibliografía
Si te ha sido de utilidad este post, te agradecería que me apoyases en Patreon (donando una cantidad aunque sea poca ya sea una vez, o apoyándome mensualmente). Tener una web, dominio, hosting, no es gratis y me apoyas a seguir ayudando con la difusión de educación libre. Apóyame en Patreon! Mil gracias!!
¿Te ha parecido útil este artículo?

